Topic 3: Inequalities

Introduction to Inequalities

Inequality tells us about the relative size of two values.

Mathematics is not always about "equals"! Sometimes we only know that something is bigger or smaller

For Example;

Alex and Billy have a race, and Billy wins!

What do we know?

We don't know how fast they ran, but we do know that Billy was faster than Alex:

Billy was faster than Alex

We can write that down like this:

b > a

(Where "b" means how fast Billy was, ">" means "greater than", and "a" means how fast Alex was)

We call things like that inequalities (because they are not "equal")

Greater or Less Than

For Example;

Alex plays in the under 15s soccer. How old is Alex?

We don't know exactly how old Alex is, because it doesn't say "equals"

But we do know "less than 15", so we can write:

Age < 15

The small end points to "Age" because the age is smaller than 15.

... Or Equal To !!

For Example;

You must be 13 or older to watch a movie.

The "inequality" is between your age and the age of 13.

Your age must be "greater than or equal to 13", which is written:

Age ≥ 13

Equal Greater or Less Than

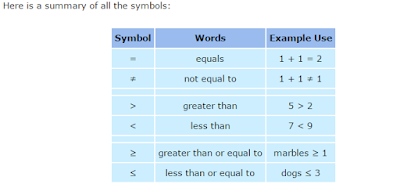
As well as the familiar equals sign (=) it is also very useful to show if something is not equal to (≠) greater than (>) or less than (<)

Less Than and Greater Than

The "less than" sign and the "greater than" sign look like a "V" on its side, don't they?

To remember which way around the "<" and ">" signs go, just remember:

BIG > small

small < BIG

For Example;

10 > 5

"10 is greater than 5"

Or the other way around:

5 < 10

"5 is less than 10"

Do you see how the symbol "points at" the smaller value?

... Or Equal To ...

To show this, we add an extra line at the bottom of the "less than" or "greater than" symbol like this:

The "less than or equal to" sign: ≤

The "greater than or equal to" sign: ≥

All The Symbols

Why Use Them?

Because there are things we do not know exactly...

...but can still say something about.

So we have ways of saying what we do know (which may be useful!)

For Example;

John had 10 marbles, but lost some. How many has he now?

Answer;

He must have less than 10:

Marbles < 10

If John still has some marbles we can also say he has greater than zero marbles:

Marbles > 0

But if we thought John could have lost all his marbles we would say

Marbles ≥ 0

In other words, the number of marbles is greater than or equal to zero.

Topic 2: Logarithm

The Rules of Logarithm

1. Proof of Product Rule Law:

logₐ (MN) = logₐ M + logₐ N

Let logₐ M = x ⇒ aˣ = M

and Iogₐ N = y ⇒ aʸ = N

Now aˣ * aʸ = MN or, aˣ⁺ʸ = MN

Therefore from definition, we have,

logₐ (MN) = x + y = logₐ M + logₐ N [putting the values of x and y]

Corollary: 

The law is true for more than two positive factors, For Example;

logₐ (MNP) = logₐ M + logₐ N + logₐ P

since, logₐ (MNP) = 1ogₐ (MN) + logₐ P = logₐ M + logₐ N + logₐ P

Therefore in general, logₐ (MNP....) = logₐ M + logₐ N + logₐ P + ....

Hence, the logarithm of the product of two or more positive factors to any positive base other than 1 is equal to the sum of the logarithms of the factors to the same base

2. Proof of Quotient Rule Law:

logₐ (M/N) = logₐ M - logₐ N

Let logₐ M = x ⇒ aˣ = M

and logₐ N = y ⇒ aʸ = N

Now aˣ/aʸ = M/N or, aˣ-ʸ = M/N

Therefore from definition we have,

logₐ (M/N) = x - y = logₐ M- logₐ N [putting the values of x and y]

Corollary: 

logₐ [(M × N × P)/R × S × T)] = logₐ (M × N × P) - logₐ (R × S × T) = logₐ M + Iogₐ N + logₐ P - (logₐ R + logₐ S + logₐ T) 

The formula of quotient rule [logₐ (M/N) = logₐ M - logₐ N] is stated as follows: The logarithm of the quotient of two factors to any positive base other than I is equal to the difference of the logarithms of the factors to the same base.

3. Proof of Power Rule Law:

Iogₐ Mᶰ = n Iogₐ M

Let logₐ Mᶰ = x ⇒ aˣ = Mᶰ

and logₐ M = y ⇒ aʸ = M

Now, ax = Mᶰ = (aʸ)ᶰ = aᶰʸ

Therefore, x = nʸ or, logₐ Mᶰ = n logₐ M [putting the values of x and y]. 

4. Proof of Change of base Rule Law:

logₐ M = logb M × logₐ b

Let Iogₐ M = x ⇒ aˣ = M,

logb M = y ⇒ bʸ = M,

and logₐ b = z ⇒ aᶻ = b.

Now, aˣ = M= bʸ - (aᶻ)ʸ = aʸᶻ

Therefore x = ʸᶻ or, logₐ M = Iogb M × logₐ b [putting the values of x, y, and z].


Corollary:

(i) Putting M = a on both sides of the change of base rule formula [logₐ M = logb M × logₐ b] we get,

logₐ a = logb a × logₐ b or, logb a × logₐ b = 1 [since, logₐ a = 1] 

or, logb a = 1/logₐ b

For Example; the logarithm of a positive number a with respect to a positive base b (≠ 1) is equal to the reciprocal of logarithm of b with respect to the base a.

(ii) From the log change of base rule formula we get,

logb M = logₐ M/logₐ b

For Example; the logarithm of a positive number M with respect to a positive base b (≠ 1) is equal to the quotient of the logarithm of the number M and the logarithm of the number b both with respect to any positive base a (≠ 1).


Note: 

(i) The logarithm formula logₐ M = logb M × logₐ b is called the formula for the change of base.

(ii) If bases are not stated in the logarithms of a problem, assume same bases for all the logarithms.

Topic 1: Indices

Rules of Indices

An indices is a number with a power, For example; am, a is called the base and m is the power. The power is also often referred to as the “index” or “exponent”.

Fact

[Indices rules only apply when the base is the same for all terms. This is very important to remember.]

Below is the indices rules that you should familiar with. Notice that the a is constant within each rule.

First indices rule:

This is a very popular rule in indices. This is known as the multiplication rule. Powers can be used to indicate how many times a base has been multiplied by itself. 

For example;

a × a × a × a × a = ?

...tells us that ‘a’ has been multiplied by itself 5 times. We write this as;

a × a × a × a × a = a⁵

The power ‘5’ is the number of times that a has been multiplied by itself. In the rule we can replace m and n with 4 and 3 respectively;

a⁴ × a³ = ?

Tip!

[In multiplication rule we only need to add the powers]

Since the base is the same in both terms the multiplication is just a continuation. To observe this expand the expression;

a × a ×  a × a × a × a × a = a⁴⁺³ = a⁷

The total number of as in the expansion is equal to the sum of powers in the question. This proves that an aⁿ × a^m = a^n+m

Second indices rule:

This rule of indices is known as the power of a power. A number with a power can be raised to a power, Example; a⁵ to the power 2.

This expression simply means;

a⁵ × a⁵ = ?

...we know that the first rule tells us that we should add the indices power together for multiplication;

a⁵ × a⁵ = a¹⁰

But note also that 5×2 is equal to 10. This suggests that if we have am raised to the power n we simply multiply the powers together to get the result amxn or simply amn, this is proof for the second rule. Below are some examples of how to use this rule.

For example;

(4⁵)² = ?

The power of two means that we want to have 4⁵ multiplied by itself 2 times. In this case we simply just multiply the powers together.

(4⁵)² = 4^5×2 = 4¹⁰

The answer for the above question is actually a very large number of 1048576 so you can see why it is important that you leave your answers in indices form.

This example proves the general rule of indices that (aⁿ)^m = a^nm

Third indices rule:

This rule states that for the division of two powered numbers, the result is equal the base to the power of the difference between the two powers as shown in the following.

For example;

4⁸ ÷ 4² = ?

Expand the expression first to observe what is going on.

4⁸ ÷ 4²  = 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4

                4 × 4

We can now use cancelling to simplify the expressions.

4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 = 46

4 × 4

There has been two cancellations which proves that we only need to find the difference between the two powers as shown below.

4⁸ ÷ 4² = 4^8-2 = 4⁶

Remember to leave your answers in indices, rather than the actual value. This is useful when carrying out much large/complex calculations.

Fourth indices rule:

This next rule is very obvious (well... to remember). It is not so obvious why any number to the power zero is 1, but there is a number of ways this can be proved. In this article we shall prove it by using the third indices rule.

Proof!

We know that any number divide by itself is equal to zero.

4/4 = 1 , 7/7 = 1 , 40/40 = 1    

The general idea is that a/a = 1. If this is true then that must also mean that;

a^m/aⁿ = 1       

Notice here that we can use the third indices rule of subtraction which states that;

a^m ÷ aⁿ = a^m-n

We can replace m and n by the same number such that the number in the numerator is equal to the number in the denominator. To make sure that when we divide we get 1. if we replace m and n with a single number;

(12^m)/(12^m) = 12^(m-m) = 12⁰ = 1 ≡ (12^m)/(12^m)

...or...

(12ⁿ)/(12ⁿ) = 12^(n-n) = 12⁰ = 1 ≡ (12ⁿ)/(12ⁿ)

Tip!

Dividing a number by itself = 1

Fifth indices rule:

The following indices rule deal with negative and fractional powers.

Be careful here 2^-4 is not the same as 2⁴ and it should not be related in anyway. Look at the pattern below;

2³ = 8

2² = 4

2¹ = 2

2⁰ = 1

2^-1 = 0.5

2^-2 = 0.25 = ½

2^-3 = 0.125 = ¼

By looking at the worked out indices above do you note a pattern? A negative power on any number creates a reciprocal of that number.

2^-3 = 1/2³ = 1/8 

         

The general rule for negative powers is;

a^-n = 1/aⁿ

          

^{For example;}

 2^-5/3 = ?

        

The reciprocal of;

2/3 = 3/2

     

That must mean that;

2^-5/3 = 3⁵/2

        

Next we simply power the denominator and numerator separately;

3⁵/2⁵= 243/32

Sixth indices rule:

The indices rule shown above is known as fractional indices rule. This is the simpler version but not different from the one shown below. You must know that anything to the power 1 is itself. So the expression shown below must be true;

a^½ × a^½ = a^½+½ = a¹ = a

The expression above implies that a^½ is the √a. That proves the above rule that;

a^½ = √a

It also proves that;

a⅓ = ∛a

because...

a⅓ × a⅓ × a⅓ = a¹